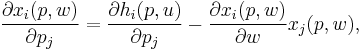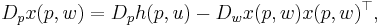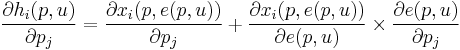Slutsky equation

The Slutsky equation (or Slutsky identity) in economics, named after Eugen Slutsky (1880-1948), relates changes in Marshallian demand to changes in Hicksian demand. It demonstrates that demand changes due to price changes are a result of two effects:

a substitution effect, the result of a change in the exchange rate between two goods; and
an income effect, the effect of a change in price results in a change of the consumer's purchasing power.

Each element of the Slutsky matrix is given by

${\partial x_i(p, w) \over \partial p_j} = {\partial h_i(p, u) \over \partial p_j} - {\partial x_i(p, w) \over \partial w } x_j(p, w),\,$

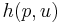where $h(p, u)$ is the Hicksian demand and 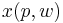$x(p, w)$ is the Marshallian demand, at price level p, wealth level w, and utility level u. The first term represents the substitution effect, and the second term represents the income effect.^[1]

The above equation is also known as the Hicksian decomposition of demand. The left hand side of the equation represents how demand for one good changes in response to price changes for another good. The right hand side of the equation says that this change is equal to the change in demand holding expenditure fixed at w* plus the change in demand when income changes multiplied by how much income has to change to keep utility constant.^[2]

The same equation can be rewritten in matrix form as

$D_p x(p, w) = D_p h(p, u)- D_w x(p, w) x(p, w)^\top,\,$

where D_p is the derivative operator with respect to price and D_w is the derivative operator with respect to wealth.

The matrix 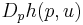$D_p h(p, u)$ is known as the Slutsky matrix, and given sufficient smoothness conditions on the utility function, it is symmetric, negative semidefinite, and the Hessian of the expenditure function.

Derivation

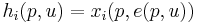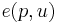While there are several ways to derive the slutsky equation, the following method is likely the simplest. Begin by noting the relationship $h_i(p,u) = x_i (p, e(p,u))$ where $e(p,u)$ is the expenditure function. Differentiating the above equation yields the following.

$\frac{\partial h_i(p,u)}{\partial p_j} = \frac{\partial x_i(p,e(p,u))}{\partial p_j} %2B \frac{\partial x_i (p,e(p,u))}{\partial e(p,u)} \times \frac{\partial e(p,u)}{\partial p_j}$

Making use of the fact that 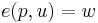$e(p,u) = w$ and

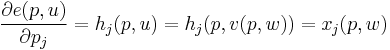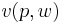$\frac{\partial e(p,u)}{\partial p_j} = h_j(p,u) = h_j(p, v(p,w)) = x_j(p,w)$ where $v(p,w)$ is the indirect utility function, we can substitute and rewrite the derivation above as the Slutsky equation.

References

^ Nicholson, W. 2005. Microeconomic Theory. 10th edn. Mason, Ohio. Thomson Higher Education.
^ Varian, H. 1992. Microeconomic Analysis. 3d edn. New York, N.Y. W.W Norton & Company, Inc

Slutsky equation

Derivation

See also

References